Силлогистика Аристотеля — это первая известная в истории модель дедуктивных рассуждений. Она применялась для ведения научных споров. В ходе такого спора доказательство выдвинутого положения защищалось с помощью ответов двух типов («согласен» или «не согласен») на любые высказывания оппонентов.
Дедуктивные рассуждения — это рассуждения от общего к частному. Суть дедуктивных рассуждений: если общее утверждение верно, то должны быть верны и частные утверждения, определяемые этим общим утверждением.
Примеры дедуктивных рассуждений:
1. Зная, что все предметы падают на землю, можно предполагать, что и подброшенный мяч также упадет.
2. Из двух априорных посылок «Все птицы имеют крылья», «Пингвин — птица» можно сделать заключение о том, что «Пингвин имеет крылья».
3. Из двух априорных посылок «Все птицы имеют крылья», «Все птицы откладывают яйца» можно сделать заключение о том, что «Некоторые существа, откладывающие яйца, имеют крылья».
Последние два примера являются силлогизмами Аристотеля.
Сущность — объект, явление, процесс, т.е. то, о чем можно утверждать. Сущности обозначаются маленькими буквами.
Пример: «пингвин», «макака», «орангутанг».
Класс — совокупность (множество) сущностей, объединенных общим именем.
Классы могут содержать бесконечное число сущностей, конечное число сущностей, а также быть пустыми. Классы обозначаются большими буквами.
Пример: бесконечный класс — «натуральные числа», конечный класс — «обезьяны», пустой класс — «летающие обезьяны».
Квантор всеобщности - если его поставить рядом с именем класса, то будет утверждаться нечто, что одновременно истинно для всех сущностей, входящих в класс.
Пример. «Все птицы имеют крылья».
Квантор существования - если его поставить рядом с именем класса, то в высказывании будет утверждаться нечто, что истинно для какого-то подмножества сущностей, входящих в класс.
Пример. «Некоторые птицы летают».
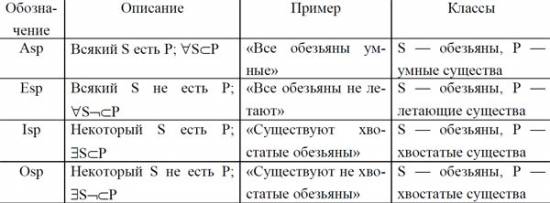
Используя составные части силлогистики Аристотеля, можно задать базовые высказывания силлогистики.
Базовые высказывания силлогистики:
Здесь S — класс сущностей, о которых что-то утверждается в высказывании, а P определяет, что именно о них говорится.
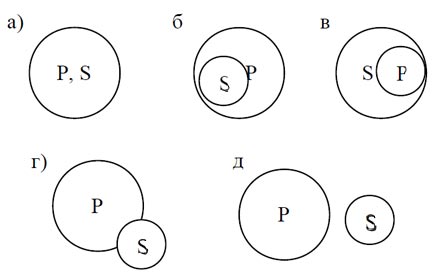
Смысл базовых высказываний можно наглядно представить с помощью жергоновых отношений:
Цель силлогистики — получение правильных рассуждений на основе исходных посылок.
Схема вывода следующая: Посылка1, Посылка2, … , Посылка N -> Заключение
Посылки и заключение задаются базовыми высказываниями, а знак -> означает, что если истинны все посылки, то истинно и заключение. Предполагается, что в N посылках участвует N+1 класс.
По количеству исходных посылок различают:
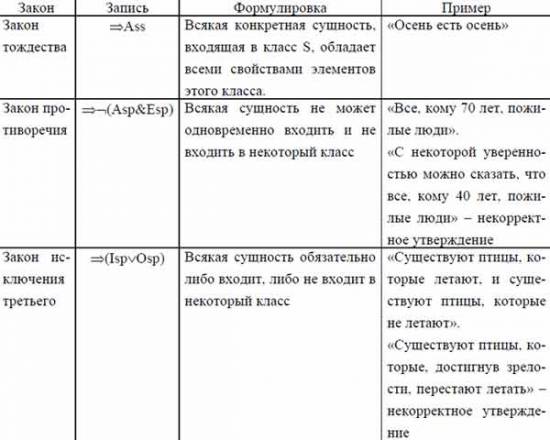
Законы силлогистики
Законы силлогистики истинны всегда и не зависят от каких-либо посылок.
Законы обращения определяют правила преобразования базовых высказываний.
Asp -> Isp - Если верно, что «Все птицы откладывают яйца», то верно, что «Некоторые птицы откладывают яйца»
Esp -> Eps - Если верно, что «Все обезьяны не летают», то верно, что «Все летающие существа не обезьяны»
Isp -> Ips - Если верно, что «Некоторые птицы летают», то верно, что «Некоторые летающие существа являются птицами»
Esp -> Ops - Если верно, что «Все обезьяны не летают», то верно, что «Некоторые летающие существа не обезьяны»
Правильность законов обращения можно проверить с помощью жергоновых отношений.

Для каждой фигуры имеется ограниченный набор правильных силлогизмов:
1) AAA EAE EIO AII AAI EAO
2) EAE AEE EIO AOO EAO AEO
3) AAI IAI AII EAO OAO EIO
4) AAI AEE IAI EAO EIO AEO
http://fevt.ru/load/sillogistika_aristotelja/31-1-0-326
Дедуктивные рассуждения — это рассуждения от общего к частному. Суть дедуктивных рассуждений: если общее утверждение верно, то должны быть верны и частные утверждения, определяемые этим общим утверждением.
Примеры дедуктивных рассуждений:
1. Зная, что все предметы падают на землю, можно предполагать, что и подброшенный мяч также упадет.
2. Из двух априорных посылок «Все птицы имеют крылья», «Пингвин — птица» можно сделать заключение о том, что «Пингвин имеет крылья».
3. Из двух априорных посылок «Все птицы имеют крылья», «Все птицы откладывают яйца» можно сделать заключение о том, что «Некоторые существа, откладывающие яйца, имеют крылья».
Последние два примера являются силлогизмами Аристотеля.
Составные части силлогистики
Составными частями силлогистики Аристотеля являются такие понятия как «сущность», «класс» и «квантор».
Сущность — объект, явление, процесс, т.е. то, о чем можно утверждать. Сущности обозначаются маленькими буквами.
Пример: «пингвин», «макака», «орангутанг».
Класс — совокупность (множество) сущностей, объединенных общим именем.
Классы могут содержать бесконечное число сущностей, конечное число сущностей, а также быть пустыми. Классы обозначаются большими буквами.
Пример: бесконечный класс — «натуральные числа», конечный класс — «обезьяны», пустой класс — «летающие обезьяны».
Квантор всеобщности - если его поставить рядом с именем класса, то будет утверждаться нечто, что одновременно истинно для всех сущностей, входящих в класс.
Пример. «Все птицы имеют крылья».
Квантор существования - если его поставить рядом с именем класса, то в высказывании будет утверждаться нечто, что истинно для какого-то подмножества сущностей, входящих в класс.
Пример. «Некоторые птицы летают».
Используя составные части силлогистики Аристотеля, можно задать базовые высказывания силлогистики.
Базовые высказывания силлогистики:
Здесь S — класс сущностей, о которых что-то утверждается в высказывании, а P определяет, что именно о них говорится.
Смысл базовых высказываний можно наглядно представить с помощью жергоновых отношений:
Цель силлогистики — получение правильных рассуждений на основе исходных посылок.
Схема вывода следующая: Посылка1, Посылка2, … , Посылка N -> Заключение
Посылки и заключение задаются базовыми высказываниями, а знак -> означает, что если истинны все посылки, то истинно и заключение. Предполагается, что в N посылках участвует N+1 класс.
По количеству исходных посылок различают:
- выводы ранга 0 — законы силлогистики;
- выводы ранга 1 — законы обращения;
- выводы ранга 2 — силлогизмы;
- выводы ранга 3 и более — сориты.
Законы силлогистики
Законы силлогистики истинны всегда и не зависят от каких-либо посылок.
Законы обращения определяют правила преобразования базовых высказываний.
Asp -> Isp - Если верно, что «Все птицы откладывают яйца», то верно, что «Некоторые птицы откладывают яйца»
Esp -> Eps - Если верно, что «Все обезьяны не летают», то верно, что «Все летающие существа не обезьяны»
Isp -> Ips - Если верно, что «Некоторые птицы летают», то верно, что «Некоторые летающие существа являются птицами»
Esp -> Ops - Если верно, что «Все обезьяны не летают», то верно, что «Некоторые летающие существа не обезьяны»
Правильность законов обращения можно проверить с помощью жергоновых отношений.
Силлогизмы
При решении силлогизмов используются так называемые «фигуры силлогизмов», которые определяют расположение классов в посылках и заключении. М – это общий класс в двух посылках.

Для каждой фигуры имеется ограниченный набор правильных силлогизмов:
1) AAA EAE EIO AII AAI EAO
2) EAE AEE EIO AOO EAO AEO
3) AAI IAI AII EAO OAO EIO
4) AAI AEE IAI EAO EIO AEO
http://fevt.ru/load/sillogistika_aristotelja/31-1-0-326